Gravitational pull
For the most fuel-efficient launch, the rocket must be launched from the equator, where the escape velocity is minimal. The escape velocity is the velocity at which a body must travel before it breaks free of the gravitational pull of a celestial body. The earth’s escape velocity is around 11.2 km/s, which is approximately 33 times the speed of sound.
The gravitational force decreases with the square of the distance, meaning that if a certain distance away from the body the gravity is only half that on the surface, at twice that distance the gravity will be four times less, eight times less, and so on.
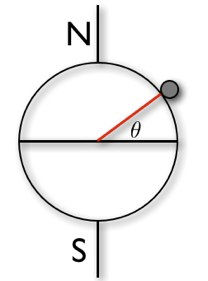
If the earth was perfectly spherical then gravity would be the same over the entire planet’s surface. The earth is not a perfect sphere though, apart from mountains and valleys. The tropics bulge out and the polar radius is around 21 km less than the equatorial one. This results in a lower gravitational pull at the equator of about 0.6%.
This can be calculated with the following formula:
g (m/s²) = 9.80616 - 0.025928 cos (2L) + 0.000069 cos² (2L) - 0.000003h
where
-
L = latitude
-
h = height above sea level (in metres)
This however is not the reason why most satellites are launched from the equator.
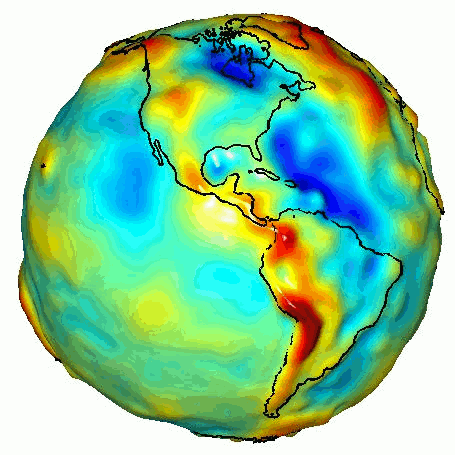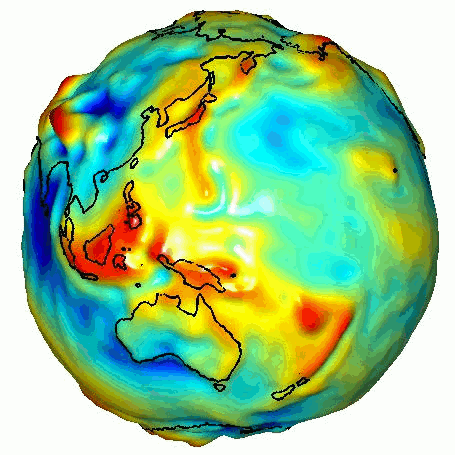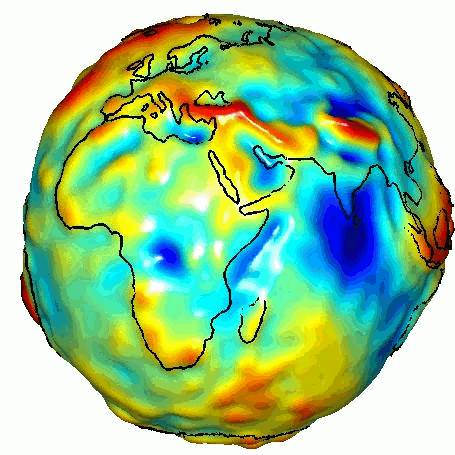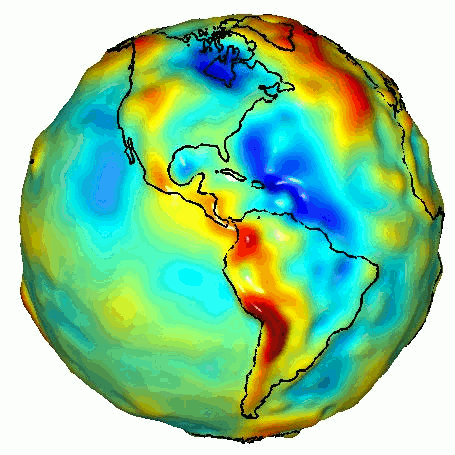
Gravitational pull around the world
Reason why an Equatorial Launch Site is Preferred
-
Many satellites are launched into geostationary orbit - this means that they appear to be fixed with respect to earth - in reality they have an orbital period of 24 hours and must also orbit above the equator. Launching from the equator puts a satellite straight into an equatorial orbit. Launching from any other latitude puts a satellite into an orbit inclined to the equator (so it won't be geostationary) and extra rocket fuel is required to adjust the orbit to an equatorial one.
-
The earth is rotating once in 24 hours - at the equator this amounts to a speed of 1670 km.hr-1 so even when a satellite is on the ground at the equator it's moving easterly at 1670 km.hr-1 or 0.463 km.s-1. The speed for orbit (500 km above the earth's surface) is 7.59 km.s-1. That's why satellites are almost always launched towards the east. A rocket launched tangentially from the Earth’s equator to the east requires an initial velocity of about 10.735 km/s relative to Earth to escape whereas a rocket launched tangentially from the Earth’s equator to the west requires an initial velocity of about 11.665 km/s relative to Earth. Moving away from the equator reduces this free speed - at the poles it is zero and in between if falls off with the cosine of the launch site's latitude. Thus launching a satellite towards the east from a site on the equator means that the earth's rotation contributes just over 6% to its final velocity. This is equally useful for interplanetary probes - which will also gain from leaving their orbit around the earth in the same direction as the earth revolves round the sun (by picking up the earth's orbital velocity).
Orbital velocity
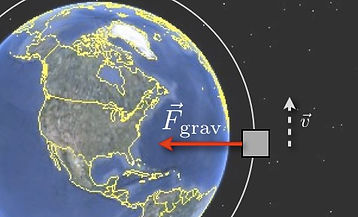
The gravitatonal force on a rocket can be calculated as follows:
An object moving in a circle has an acceleration toward the center of the cicle with a
magnitude of:
Putting these two together with Newton's Second law results in:
r in this case is the distance from the center of the Earth to the object in orbit.

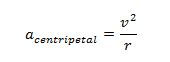
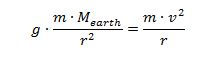
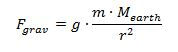
Needed Energy
First, with the assumption the Earth is not rotating. The means the rocket starts from rest. With the work-energy principle.
Here Re is the radius of the Earth (starting point of the rocket)
Now when the Earth is not rotating. The rocket has an initial velocity of:
The new formula for calculating the need work becomes:
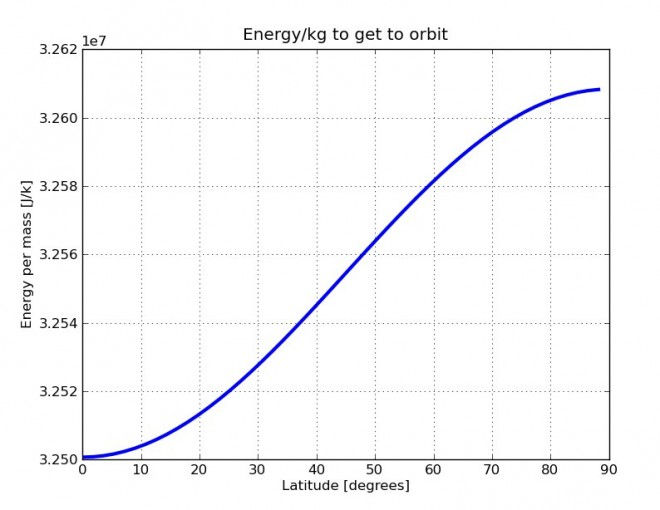
Shown below is a graph with the energy needed per kg of mass, to put someting in low-Earth orbit (an altitude of about 300 km) as a function of the latitude.